Bienvenidos al blog!

Esperamos que todo el contenido sea muy útil :D

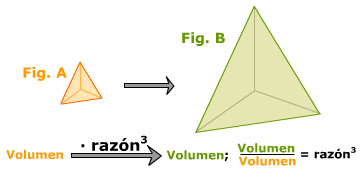
3.3 RAZON DE SEMEJANZA EN VOLUMEN

Si dos figuras A y B son semejantes, el cociente entre el volumen de B y el de A es el cubo de la razón de semejanza de la figura B  sobre la A.

 Ejercicios resueltos

   

 ¿Cuál es la razón de una semejanza que

    convierte un segmento de longitud 5 m en
     otro de longitud 3 m?
  
Solución: La razón de semejanza es el cociente entre
      longitudes homólogas.
       Razón = 3/5=0,6

Calcula la longitud del segmento homólogo

   al de 4 m, sabiendo que al aplicar la
   semejanza de esa misma razón, un
   segmento de 3 m se transforma en uno de
   7,2 m.
  Solución: Razón =7,2/3=2,4
   x=4·razón=4·2,4=9,6 m

En una semejanza un segmento de 5m se
transforma en otro de 10m. En la figura
transformada hay un segmento de longitud
  8m ¿Cuál es la longitud del segmento del
  que proviene?

 Solución: Razón =10/5=2
  x·razón=8 => x·2=8;
  x=4
   

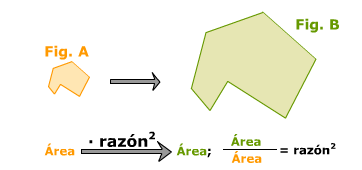
3.2 RAZON DE SEMEJANZA EN ÁREAS

Si dos figuras A y B son semejantes, el cociente entre el área de B y el área de A es el cuadrado de la razón de semejanza de la figura B sobre la A. 

                                  

Vídeo Explicativo:

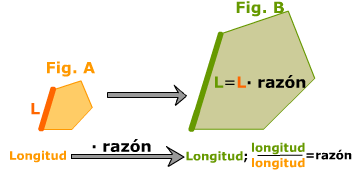
3.1 RAZON DE SEMEJANZA EN LONGITUDES

Si dos figuras A y B son semejantes, se llama razón de semejanza de la figura B sobre la A al cociente entre la  longitud de un segmento de la figura B y la de su homólogo en la figura A.

La razón de semejanza define la homotecia que transforma la figura A en la B.

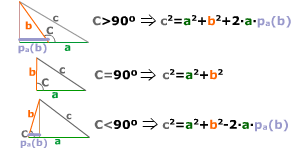
2.3 TEOREMA DE PITAGORAS GENERALIZADO

Se trata de aplicar el teorema de Pitágoras, que solo podemos utilizarlos en triángulos rectángulos, poder aplicarlos en triángulos obtusángulos y acutángulos.

Por si se nos ha olvidado el teorema de Pitágoras os dejo un vídeo explicativo para recordarlo 

Teorema de Pitágoras à Hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos

1.Para triángulos obtusángulos

 2.Para triángulos rectángulos

       3.Para triángulos acutángulos

2.2 TEOREMA DE LA ALTURA

Para hallar la altura de un triangulo rectángulo aplicamos este teorema que dice que El cuadrado de la altura que descansa sobre la hipotenusa es igual al producto de las proyecciones de los catetos sobre la hipotenusa

Ejercicio resuelto

Se quiere construir un jardín forma de triángulo rectángulo. Se sabe que la

altura y la proyección de un lado sobre el lado mayor (hipotenusa) miden 15,3 m y 8,1 m, respectivamente. Calcula el perímetro del jardín.

SOLUCIÓN: (Haz click sobre ella para agrandarla)

Para entender mejor este teorema os dejo un video que explica como realizar un ejercicio

2.1 TEOREMA DEL CATETO

Para hallar uno de los catetos de un triangulo utilizamos el teorema que dices que el cateto al cuadrado es igual a la hipotenusa por la proyección del cateto sobre ella

Para triángulos rectángulos

 

Para triángulos obtusángulos y acutángulos

 

Comprobación del teorema del cateto

Haz click aquí para obtener ejercicios

Ejercicio resuelto: (Haz click encima para verlo más grande)